Regions

When the Mac first debuted in 1984, it introduced ordinary consumers to the concept of overlapping windows. If I recall correctly the Apple Lisa had them, too, but ordinary consumers couldn't afford that innovative product. The offering before then was an apportionment of the screen into non-overlapping rectangular chunks, promoted by the researchers at Xerox PARC (at least that's how I heard the story). What made the Mac's windows possible was the underlying region technology, developed and patented by Bill Atkinson at Apple (US Patent 4,622,545).

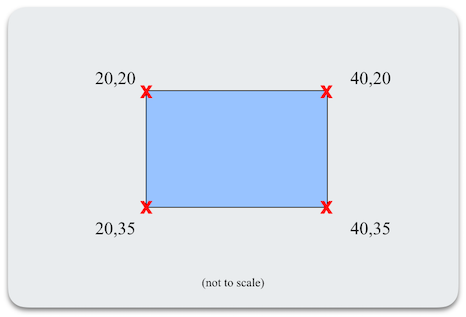
A region is a data structure that describes an area of screen geometry (or, for most systems, a collection of pixels) using a series of inversion points. Organized by rows, the first x value of a pair inverts the state of whether subsequent pixels are either in or out of the region. A simple rectangular region would consist of just two rows, each with just two inversion points. In the diagram below, the row at 20 would have two x values, one at 20 and one at 40, including the pixels between the two x values as part of the area being described. That status persists until row 35, whereupon the inversion points at 20 and 40 are removed, so the pixels between them are no longer included.

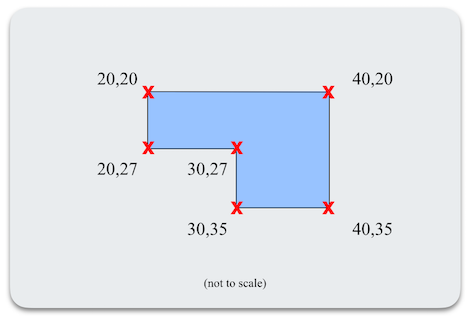
Next, let's add another pair of inversion points, one lining up with the first inversion point and one in the middle of the rectangle. We also have to adjust the bottom row inversion point to match. Here's what's produced.

The real power of this data structure arises from the calculations it enables. For example, consider the task of determining if a mouse click has happened inside a window's area. As a first approximation we could use the bounding box of its region. For the example above that would be the rectangle from (20,20) to (40,35). But if the window was partially obscured, and we know the mouse click happened within the bounding box, what then? Using the Atkinson data structure, count the number of inversion points that lie above and to the left of the mouse click. If that number is odd, the click happened within the region. If it's even, the click happened outside the region. This calculation is very fast, and it helped make early Mac's very responsive to user interactions.

But as Bill's patent teaches, regions have much more to offer for the creation of overlapping window desktops. If you have several regions, each one describing the pixels belonging to a window on the screen, you could determine the region for an underlying window by starting with its bounding box and subtracting the regions of all the windows lying atop it. The true power of Bill's innovation arises from the fact that a simple logic test yields four very useful region operations: add, subtract, intersect, and xor. Together these operations enable everything needed to create overlapping windows. Better yet, they are relatively fast compared to other methods, and thus were suitable for use on early Macs.

Guildhall Regions

When I first considered taking over the desktop, I had to consider how to handle overlapping windows. Having implemented regions a couple of times I knew how to code them, and although other techniques are available with the power modern GPUs offer, I also wanted to use regions as one of the geometric forms for drawing. I would have loved to use the Taligent construct called the TGArea, a graphics primitive for constructive area geometries, but at the time it was still under patent protection. Sad you can't use your own patent, but that's life. Using paths was another possibility, and yes they are a nice way to describe arbitrary areas, but, conceptually, the region operations offer (in my opinion) easier access to commonly encountered geometries.

But there is an architectural conflict between the pixel-oriented structure of traditional regions and a region that can be used as part of a resolution independent graphics package. It's easy to transform geometric entities such as lines and polygons for the purposes of scaling or rotation. If left as inversion points, scaling up a traditional region would show all the pixelated boundaries. That's not the desirable effect.

So I stepped back from pixels and gave some consideration to a region data structure based on double precision floating point numbers. Like its traditional counterpart it had to accommodate operations on regions. But it also had to translate to an element the host OS could use to effect clipping. On macOS the clipping is effected with paths, and fortunately they are floating point based. They respond to transformation the same way as the drawing geometries do. So for Mac, at least, the problem resolved into providing typical region operations on the Guildhall side and producing a path-oriented result on the host side.

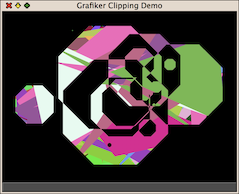
My solution drew upon a project I worked on for a now subsumed chip software company called VLSI Technology. The task there was to print chip geometries, adding overlapping polygons together to produce a uniform output. The algorithm, supplied to me by Dick L, involved resolving the geometries into edges and pairing those edges up, keeping track of wrap counts and eliminating all edges that ended up on the interior of a given polygon. As it turned out, it was exactly what I needed, because the edges fit nicely with the Atkinson region operation model. It was incredibly tricky code (at least for me), and there's still one failing test case I haven't yet been able to resolve, but in practice it has worked quite well. Here are some clipping examples from the test applet Grafiker.

Eventually I will probably move to the technological underpinnings of TGArea, because it is a better solution and the patent is now expired. It is true that the TRegion class can be scaled and transformed, but under extreme transforms it will begin to show its rough edges, both literally and figuratively. A TArea class can defer edge processing until after transformation, giving a more pleasing result.

Constructible Classes

• TRegion